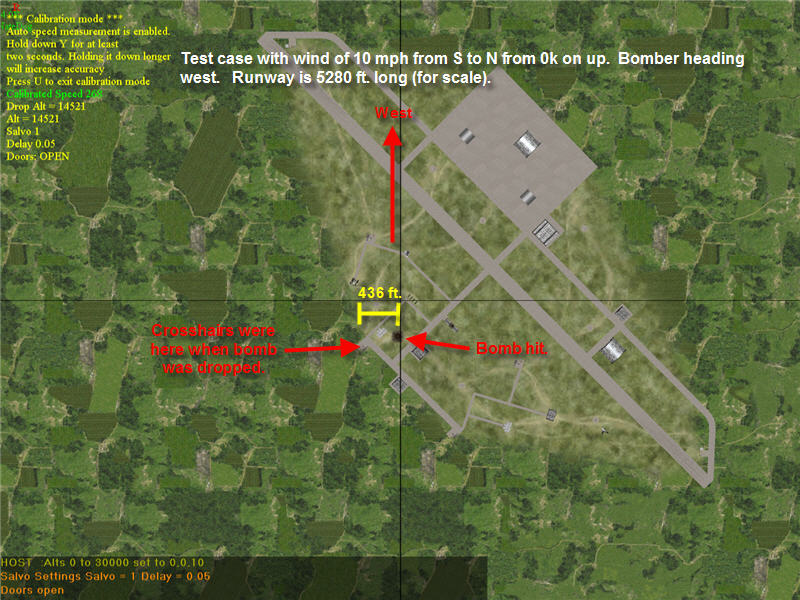
Image of results of test 1.
This document describes a model for bombing in wind in Aces High when using "easy mode" bombsight calibration. It allows you to, based on altitude and crosswind speed, come up with a number that predicts approximately how far from the crosshairs of your bombsight your bombs will hit. It gives you a simplified model of how to account for wind.
Important note: none of this is necessarily applicable to the "hard mode" bombsight. This document is for the "easy mode" bombsight only.
"Easy mode" calibration is the mode where the pilot has only to go into the bombsight, press "u", press "y" for several seconds, then press "u" again. This is as opposed to "hard mode" calibration where the pilot has to keep the sight crosshairs fixed on a ground feature during calibration. From here on out, I will call it just the "bombsight" without reference to "easy mode" or "hard mode", with the understanding that I'm always talking about "easy mode" here.
When your bombsight is properly calibrated, it means that your bomber has not accelerated, decelerated, gained, or lost altitude since you calibrated. It means that you have calibrated while your bomber was in steady flight and are still in that same steady flight. When your bombsight is properly calibrated, the crosshairs predict quite closely where on the ground your bombs will hit -- as long as there is no wind in the environment.
If there is wind, you will find that your bombs do not hit where the crosshairs predict they will -- they are off by an amount that increases as wind speed increases and as altitude increases. If you knew how much and in which direction, you could account for it during your drop. If you knew, for example, that your bombs would hit 200 feet to the left of your crosshairs, you could line up 200 feet to the right of your target, drop your bombs, and hit the target.
The model described below is not exact. It does not take into account every physical effect upon the bomb as it drops, and thus the prediction it gives will not match the actual bomb strike position exactly. However, under a lot of circumstances, it is reasonably close, and it generally will tell you to within about +/- 10% how far to the left or right from your crosshairs the bomb will hit.
There are two things that the bombsight does not do. It doesn't take into account wind layers through which your bomb travels as it drops away from your bomber, and it doesn't take into account any sideways drift of your bomber relative to the ground. When bombing with no wind, the bombsight is very accurate. If there is wind, however, you find the following things. If there is a headwind that your bomb has to travel through on its way to target, it falls short; if a tailwind, it falls long. These are easier to deal with as most bombers allow you to drop more than one bomb, and so you can drop a string of bombs to bracket the target without getting fancy on any extra calculations. This also solves the problem of not having a bombsight that is perfectly calibrated.
Crosswinds are a different matter. If your bombs fall to the side, even if you drop a long string of bombs, you will miss. This is what really needs to be accounted for. Fortunately, there is a simple model that can do it reasonably well.
The model is based on the following observations.
1. If you take up a bomber and set a 10 mph crosswind to the right (including at your bomber's altitude) and drop, the bombs hit off to the right pretty much under your bomber as it passes directly over the impact point. In other words, the bombsight simply didn't take into account the sideways motion of the bomber in the initial conditions of the bomb drop.
2. Take up a bomber to 11k and approach a target from the east. Set a 10 mph crosswind from 0 to 10k -- but set no wind from 10k on up. In other words, your bomber has no sideways travel, but the bomb will travel most of its distance to the target through a crosswind. When you do this, you find that your bombs drift a negligible amount to the side.
3. For the calculated paths of WWII bombs, air resistance is a much smaller effect than gravity. See below for more details on this.
Thus, a model that can help with calculating sideways drift of bombs can be a simple one that (1) neglects the bomb being accelerated sideways by lower-down wind layers through which it passes and (2) that simply takes into account the initial sidways velocity of the bomb.
Let d = distance to the side of the crosshair point that the bomb will hit. d = v_c * t, where v_c is the sideways velocity of the bomber and t is the time from drop until impact. t can be estimated from the dropping of the bomb just under the influence of gravity, where h = 0.5 * g * t^2 governing the altitude of the bomb vs. time from drop and where g is the gravitational acceleration. t = sqrt(2 * h / g). t [seconds] = sqrt(2 * h [feet] / 32 [ft/s^2]). v_c = v * sin(theta), where v is the wind velocity and theta is the angle between your heading and the wind direction. d = v_c * 5280 / 3600 * t, where d is in feet, v_c in mph, and t in seconds.
Thus, the model is
d = v_c * sqrt(2 * h / 32) * 5280 / 3600,
where d is the distance in feet to the side of the crosshairs the bombs will hit, h is altitude above target in feet, and v_c is the mph of the crosswind component. h is your bomber altitude minus the target altitude. v_c can be obtained from the E6B under "Wind" as the "right cross" or "left cross" crosswind readings.
As an example, here is a table of d at various altitudes assuming a 5 mph crosswind. For a crosswind of v_c (i.e., other than 5 mph), you can calculate d_new as d_table * v_c / 5. Thus, if the crosswind were 10 mph, the d values would be double.
| Altitude from target (feet) | Time to impact (sec) | d (feet) |
| 5000 | 17.7 | 130 |
| 10000 | 25.0 | 183 |
| 15000 | 30.6 | 224 |
| 20000 | 35.4 | 259 |
In the first test, a B-24 was taken up to 14,500 ft altitude. Travelling west, it approached a field that is at altitude 0. Wind was set to be 10 mph from south to north, with this wind layer from the ground all the way up. The B-24 was flown for one sector (25 miles) at its altitude and heading west to get it into steady-state before calibrating the bombsight. Then a single bomb was dropped when the crosshairs were over a target. When directly over the target, a picture was taken of the bomb hit so that its impact point could be compared to the model's prediction. The image is below. The model predicts 441 ft side offset, and the measured value was 436 ft (with about +/- 20 feet of uncertainty in calculating the value from the image).

Image of results of test 1.
The second test was done to show that bomb side offset is mainly dependent on the wind layer the bomber is in and largely independent of wind layers underneath the bomber. In the second test, a B-24 was taken up to 14,500 ft altitude. Travelling west, it approached a field that is at altitude 0. Wind was set to be 10 mph from south to north from 14k on up and 10 mph from north to south from 0 to 14k. Thus, the B-24 still has the same 10 mph sideways drift as in test 1, but the layer immediately below the bomber and all the way to the ground is a crosswind in the opposite direction. Thus, the bomb has the same initial drop conditions, but there is a 20 mph difference in the sideways wind the bomb experiences through nearly its entire drop, and the crosswind it sees during its drop is exactly opposite the direction of test 1. The B-24 was flown for one sector (25 miles) at its altitude and heading west to get it into steady-state before calibrating the bombsight. Then a single bomb was dropped when the crosshairs were over a target. When directly over the target, a picture was taken of the bomb hit so that its impact point could be compared to the model's prediction. The image is below. The model predicts the same 441 ft side offset, and the measured value was 414 ft (with about +/- 20 feet of uncertainty in calculating the value from the image). The difference between measured values in test 1 and test 2 is 22 ft, in the direction of and in line with the smaller perturbation of wind acceleration calculated in the "More Details" section (which would estimate the delta to be approximately 2 * 17 = 34 ft.).
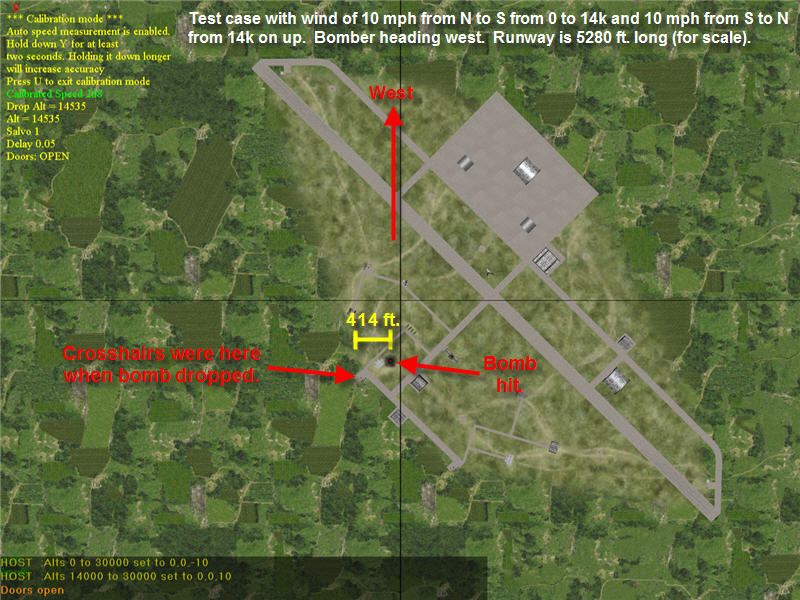
Image of results of test 2.
The third test was one done with a Ju 88 at 11k heading west. The wind was set to be 0 mph from 10k on up, and 30 mph from south to north from 0 to 10k. The bomber dropped a string of bombs down the runway, and the bombs hit down the runway, along the vertical crosshair of the bombsight. This also indicates that the effect of a crosswind under the bomber has negligible effect on side offset.
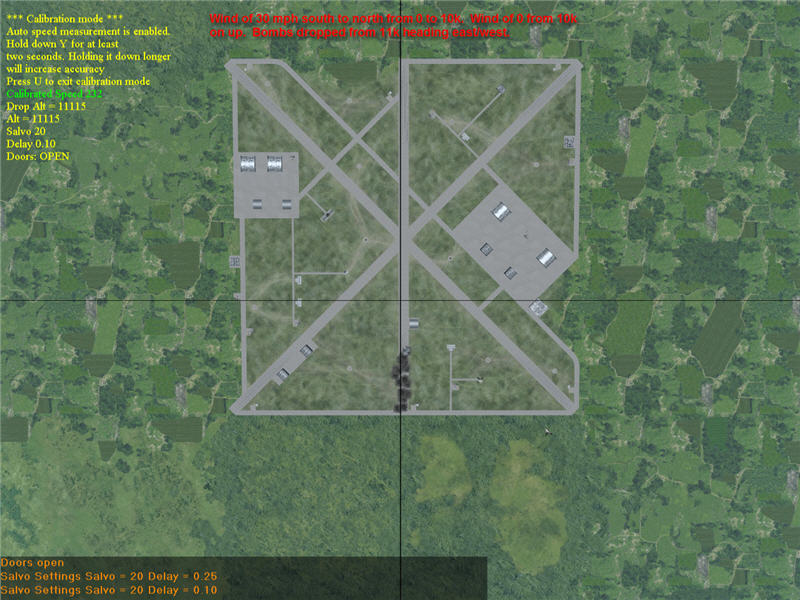
Image of test 3 results.
Once your bomb leaves your bomber, it is under the influence of two forces: gravity and air resistance (or "drag"). The gravitational force is F_g = m * g, where m is the bomb's mass and g is the acceleration of gravity. The force of air resistance can be modelled as F_D = 0.5 * rho * v^2 * A * C_D, where rho is air density, v is velocity of the object through the air, A is the effective area of the object, and C_D is the coefficient of drag.
For a 250 lb bomb, let's estimate some of these numbers. Let m = 250 lb = 113 kg. g = 9.8 m/s^2. Under standard conditions, rho is about 1.23 kg/m^3 at sea level, 1.06 at 4500 ft. altitude, and 0.74 at 15,000 ft. For a 250 lb bomb (the US AN-M57 bomb, say), diameter is 11 inches = 0.28 m, so frontal area = A = pi * (0.28/2)^2 m^2 = 0.062 m^2. For a smooth sphere, C_D is 0.1. For an airship or blimp, C_D is about 0.02. Let's estimate that a 250 lb bomb, which is more streamlined than a sphere but perhaps not as streamlined as a blimp, has C_D = 0.05.
Let's estimate how big F_g and F_D are, so that we know what the magnitudes of the forces are we are dealing with. F_g = 113 * 9.8 = 1110 N (Newtons). For F_D, let's use a rho at 4500 ft (as a representative middle altitude as the bomb falls) and v = 400 mph (as a representative middle velocity of a bomb as it falls) = 179 m/s. Then F_D = 0.5 * 1.06 * 179^2 * 0.062 * 0.05 = 53 N. So, the magnitude of the force of drag is about 5% of the maginitude of the force of gravity. We expect gravity, then, to be the main effect, with drag almost a perturbation upon that.
Nevertheless, the bombsight in Aces High, when calibrated correctly in "simple mode", figures in the effect of drag when there is no wind. It takes into account the forward speed of your bomber and the vertical distance between your bomber and the target and calculates everything, integrating the forces to predict path of the bombs. It does not take into account any wind under your bomber, and it does not take into account sideways drift of your bomber if your bomber is in a crosswind (i.e., misses that initial sideways velocity of the bomb). So, these two effects -- (1) unaccounted-for wind between your bomb and the target and (2) crosswind giving your bomb intial sideways drift -- are things that can cause bombs to hit away from where the bombsight predicts.
Let's discuss effect 1 first. Because F_D is already a much smaller effect than F_g, when there is unaccounted-for wind under your bomber, it is thus a perturbation on an already smaller effect. How big is this perturbation? A 10 mph headwind right under your bomber would mean that, while the bombsight thinks v is 400 mph as a typical value as the bomb drops through its trajectory, it is actually 410 mph. F_D will be 410^2/400^2 = 1.05 times larger at that point than the bombsight thinks it would be. This is thus an effect that is 5% of 5% (or 0.25%) of F_g. A 10 mph crosswind right under your bomber would mean, v = sqrt(400^2 + 10^2) = 400.125 mph. F_D will be 400.125^2/400^2 = 1.0006 times larger at that point than the bombsight thinks it would be. This is thus an effect that is 0.06% of 5% (or 0.003%) of F_g. Thus headwind and tailwind components are a larger effect (causing bombs to fall short or go long) than are winds that accelerate sideways motion of the bomb.
Let's see how large sidways acceleration of a bomb due to a crosswind is. A rough approximation would be to use maximum sideways force through the whole drop. Let's use a crosswind velocity of 10 mph and F_D as calculated above with the bomb going a representative 400 mph, to get F_D_side = side component of F_D = F_D * (10 / 400) = 53 * (10 / 400) = 1.3 N. The distance moved under the effect of a constant force is (from F = m * a), d = 0.5 * (F / m) * t^2. A 1.3 N force acting on a 113 kg object for, say, 31 seconds (approximate time for a 15k drop), would cause it to travel d = 0.5 * (F_D_side / m) * t^2 = 0.5 * (1.3 / 113) * 31^2 = 5.5 m = 17 feet. This is an estimate of how far a bomb would hit to the side of the crosshairs if (1) your bomber were in a layer that had no wind but (2) immediately below the bomber were a crosswind of 10 mph from there on down to target. This is a minor and negligible effect.
Let's discuss effect 2. Effect 2 -- sideways drift of your bomber -- is an effect that alters the initial conditions of the drop. This effect was the one we already talked about in "The Model" section above. It is a v * t sort of effect, and its an order of magnitude greater than effect 1.